Un café entre escoceses y la función social del actuario
A comienzos del Siglo XIX, un grupo de escoceses se citó en el Royal Exchange Coffe House de Edimburgo con algo en común: el temor propio de quienes están a punto de combatir en el frente de las Guerras Napoleónicas. En esta reunión decidieron acordar que, en el caso de fallecimiento de algún integrante, su viuda y sus hijos recibirían una ayuda monetaria para afrontar la pérdida de la persona de la que tenían una dependencia económica. Así, crearon la primera mutualidad escocesa de seguros de vida, una empresa que 200 años más tarde posee más de 6 millones de clientes en todo el mundo.
La necesidad de cubrirse ante un riesgo no es algo particular de este grupo de escoceses, sino que ha acompañado a los seres humanos desde el comienzo de sus tiempos: Desde riesgos relacionados con la cosecha en pequeñas sociedades del Neolítico abordados mediante la denominada “economía del regalo”, hasta multinacionales actuales cubriéndose de ataques a sus sistemas mediante seguros cibernéticos comprados en el “Lloyds” de Londres.
En este contexto, la profesión actuarial nació con el objetivo de cubrir tal necesidad, los actuarios son los encargados de crear modelos matemáticos y financieros, para cuantificar el riesgo y que la sociedad se pueda cubrir ante el mismo. De esta forma, los actuarios permiten reducir la incertidumbre a las personas, siendo esta su principal función social.
Tradicionalmente, los actuarios se han dedicado principalmente al estudio de los riesgos de mortalidad y de longevidad en el Ramo de Vida y a diferentes riesgos de daños patrimoniales como el de automóviles u hogar en el Ramo de No Vida. Si bien es cierto que estos riesgos siguen siendo relevantes, en los últimos años, según avanza la sociedad, los actuarios deben abordar el estudio de nuevos riesgos, como el cibernético mencionado anteriormente o el riesgo del Cambio Climático.
Con relación a este último, ya en la primera edición del International Panel on Climate Change (IPCC) la cual tuvo lugar en 1990, se le había otorgado un papel importante a la industria aseguradora. Concretamente, se le asignaba la labor de señalización de los riesgos y la minimización del impacto económico de las pérdidas generadas. Sin embargo, inicialmente solo algunas reaseguradoras como MunichRe o SwisRe se involucraron en este estudio (Collier, 2021). Esta pasividad por parte del resto de la industria ha llegado a su fin drásticamente en los últimos años.
Recientemente, se ha experimentado el auge de iniciativas que relacionan el cambio climático con las ciencias actuariales mediante colaboraciones entre gobiernos nacionales, ONGs, fundaciones, organizaciones internacionales y la industria aseguradora privada. Por ejemplo, la ONU y el World Bank realizan varios índices regionales, nacionales e internacionales de riesgo catastrófico climático. También el grupo de líderes del G7 lanzó una iniciativa conocida como InsurResilience para extender el acceso a coberturas a 400 millones de personas que vivían en países pobres.
Sin embargo, la mayoría de estas iniciativas han estado dirigidas hacia el riesgo catastrófico y en general a la rama de No Vida, dejando el estudio del efecto del cambio climático en riesgos como el de mortalidad o longevidad ignorado. Esta brecha de investigación ha supuesto una gran motivación para la realización de este trabajo, el cual aspira a estudiar el efecto que ha tenido, está teniendo y tendrá el cambio climático en los riesgos asociados con las vidas de las personas.
Un viaje al Oeste y la reconsideración del uso de la media
De las pocas investigaciones actuariales previas relacionando el cambio climático con el riesgo de mortalidad, se puede extraer que la temperatura es la variable que mejor actúa como “proxy” del efecto del Cambio Climático en el riesgo de mortalidad y que el grupo más vulnerable es el de personas con una edad superior a los 80 años (Huang, 2011).
Centrándonos en la temperatura, en este trabajo se han recadado los datos de las temperaturas diarias en cada una de las Comunidades Autónomas de España en los últimos 100 años. Partiendo de una novedosa metodología que considera las estadísticas de la distribución de temperaturas a lo largo de un año como realizaciones de un proceso estocástico, se pueden investigar tendencias en las propias características. Esto es relevante porque en la literatura previa se emplea la media como la característica principal en el estudio de la relación con la mortalidad (Seklecka, 2017), pero este trabajo se pregunta: ¿Por qué usar la media?
Es cierto que la media es una buena característica de una distribución y que, en el supuesto de estar ante una distribución Normal, la media es también la mediana. Sin embargo, esta característica en algunos casos puede no ser adecuada. Por ejemplo, imaginemos que, en el Lejano Oeste, un vaquero de nombre Woody tiene cierto gusto por las estadísticas y se ha de batir en un duelo. Woody consigue anticiparse a su adversario al disparar dos balas muy rápidamente: una pasando 2 metros a la izquierda y la otra 2 metros a la derecha de la cabeza de su rival. Woody podría dejar de disparar y exaltar triunfante a su rival: “He ganado! En promedio, estás muerto”. Sin embargo, de hacer esto, Woody perdería el duelo, debido a la irrelevancia de la media en este caso, con las consecuencias que perder un duelo conlleva.
En nuestro caso, sin duelos de por medio, el exceso de mortalidad por temperatura se encuentra en las temperaturas extremas. Es decir, las temperaturas muy bajas o las muy altas son las que pueden estar más relacionadas con la mortalidad, no los promedios anuales. Por lo tanto, este trabajo se replantea el uso de la media y se compara qué exhibe una mayor relación con la mortalidad la media de la temperatura o cuantiles de la distribución de temperatura anual, tales como el cuantil 0.05 y el 0.95 entre otros.
Con cuantil 0.95, nos referimos al percentil 95, es decir el punto tal que, una vez ordenados los días del año de menor temperatura a mayor temperatura, tendría el 95% de datos a su izquierda. Dicho de otra forma, aproximadamente se corresponde con el vigésimo día de más calor del año, de la misma forma que el cuantil 0.05 o percentil 5 se corresponde con el vigésimo día de más frío del año.
De este modo, se comienza realizando un análisis de los datos de temperaturas, y para cada una de las 17 Comunidades Autónomas, se encuentra una tendencia creciente significativa para tanto la media como los cuantiles, tal y como era esperado debido al Cambio Climático. Sin embargo, también se prueba que, en 11 de las 17 Comunidades Autónomas estudiadas, los percentiles superiores tienen tendencias mayores que la media y que los cuantiles inferiores. Es decir, los días más calurosos del año crecen a un ritmo mayor que la media del año o que los días más fríos del año. En otras palabras, el efecto del Cambio Climático es mayor en los cuantiles que en la media.
Dada esta diferencia en tendencias, el uso de la media podría infravalorar el impacto del Cambio Climático, si es que nuestra hipótesis de que los percentiles están relacionados con la mortalidad fuese cierta. Este debe ser, por lo tanto, el siguiente paso del proyecto.
Para averiguar si estas medidas están relacionadas con la mortalidad, primero se emplea la metodología Lee-Carter para extraer un índice de mortalidad en los meses más calurosos del año y un índice para los meses más fríos del año para cada Comunidad Autónoma en los últimos 20 años. El periodo de 20 años fue seleccionado como un punto intermedio entre la necesidad de tener suficientes datos para poder obtener resultados creíbles y el evitar emplear demasiados años previos al comienzo de la década de los 2000. Esto es debido a que a principios de la década de los 2000, varias olas de calor en Europa tuvieron lugar en Europa y sus efectos fomentaron iniciativas gubernamentales que aumentaron la adaptabilidad al calor de las poblaciones, haciendo los datos anteriores inadecuados si no se tuviese esto en cuenta.
Seguidamente, con estos índices de mortalidad se estudia la relación (correlación y cointegración concretamente) con las medidas previamente mencionadas. Por un lado, se estudia si la reducción en frío en los meses más fríos (tendencia creciente del cuantil 0.05) podría llevar a una reducción de las muertes por frío y, por tanto, a una reducción de la mortalidad en estos meses. Por otro lado, se estudia si el aumento de calor podría llevar a un aumento de la mortalidad en los meses calurosos del año.
Comenzando con los meses fríos del año, se obtiene que, para la mayoría de las comunidades estudiadas, no existe una correlación significativa entre la mortalidad en esos meses y su media o el cuantil 0.05 o el cuantil 0.10 anuales. Es decir, debido a la reducción del frío que está teniendo lugar como consecuencia del Cambio Climático, no existe una reducción en la mortalidad. Este resultado implica que el Cambio Climático no se puede relacionar con un riesgo de longevidad, ni de que, en el caso de encontrar una relación positiva entre el calor y la mortalidad, esta no se vería compensada por la reducción de mortalidad de los meses fríos del año.
Con respecto a los meses más calurosos del año, los resultados son bastante diferentes, ya que se prueba la correlación y cointegración en la mayoría de Comunidades Autónomas tanto para la media de esos meses como para los cuantiles 0.90 y 0.95 anuales. Concretamente, el cuantil 0.95 exhibe una correlación significativa y positiva en la gran mayoría de Comunidades. Concretamente, en 14 de las 17 Comunidades las correlaciones son más elevadas para el cuantil 0.95 que para la media de la distribución.
Atendiendo a la cointegración entre la mortalidad de los meses cálidos y el cuantil 0.95, se puede comprobar que, en todas las comunidades, salvo en Andalucía, Canarias y Madrid, el estadístico del Test de Johansen es superior al valor crítico al 1 %. Por lo tanto, para estas comunidades se puede rechazar al 1% de nivel de significación la ausencia de correlación. Para los casos de Andalucía y Madrid, se puede rechazar la hipótesis nula al 5 %, mientras que en el caso de Canarias al 10 %, constituyendo una menor evidencia en este territorio insular, probablemente debido a las peculiaridades de su clima subtropical.
Una vez demostrada la mayor correlación entre el cuantil 0.95 y la mortalidad, comparada con la correlación empleando la media de la distribución y tras probar la cointegración de esta medida con el índice de mortalidad, se pueden analizar ciertos resultados:
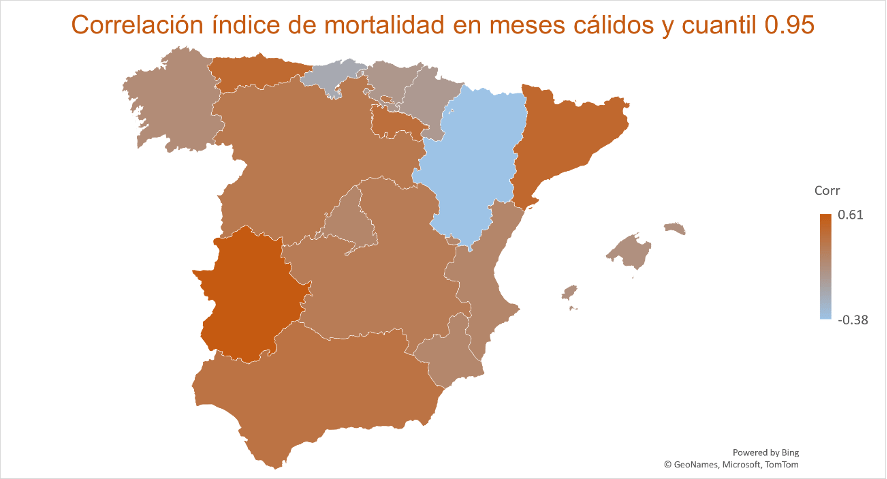
En general, las correlaciones son mayores para las comunidades del sur del país, debido a que experimentan unas temperaturas más extremas. Existen ejemplos muy llamativos como es el caso de Extremadura, donde la correlación entre mortalidad en los meses cálidos y temperatura es de 0,224 al emplear la media de esos meses como medida de temperatura, pero aumenta hasta 0.607 al emplear el cuantil 0.95 como medida para la temperatura. Este es un claro ejemplo de por qué el cuantil 0.95 debería ser empleado, en vez de la media de la distribución, para evitar un destino similar al de Woody.
Un delantero en el área y la estimación del impacto
Por lo tanto, en este punto, se ha probado que el Cambio Climático no conlleva una reducción de las muertes por reducción de frío y sí un aumento de muertes por el aumento de calor. Lo que en términos actuariales se denomina un riesgo de mortalidad, pero no de longevidad. También se ha probado la existencia de una medida de temperatura que tiene una correlación mayor con el índice de mortalidad que la media: el cuantil 0.95. Pues de la misma forma que un delantero sabe qué debe hacer cuando llega con el balón al área, un actuario conoce cuál es el siguiente paso tras probar la existencia de un riesgo y encontrar la medida que mejor lo explica: cuantificar el riesgo.
Para cuantificar el riesgo, se ha rebajado el nivel de granularidad, creando un modelo a nivel nacional, tomando la mortalidad total nacional en los 6 meses más calurosos y tomando como medida de temperatura el promedio de Madrid y Barcelona, por ser las dos ciudades más pobladas. Primeramente, se ha probado la estacionariedad del índice de mortalidad nacional resultante del Modelo Lee Carter, la cual será la variable dependiente del modelo y probando cointegración y correlación con el cuantil 0.95, que será la variable explicativa del modelo. De nuevo, a nivel nacional se repetían los resultados obtenidos a nivel de comunidades, donde el cuantil 0.95 exhibía una mayor correlación con la mortalidad que la media. Adicionalmente, se ha añadido una variable indicadora a los años afectados por el covid-19 para controlar su efecto en el análisis.
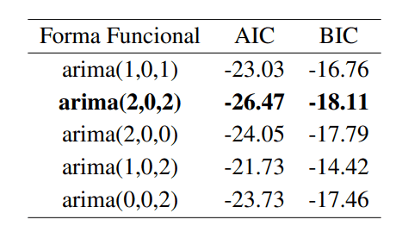
De este modo, entre las diferentes formas funcionales probadas, la seleccionada ha sido la de arima(2,0,2), atendiendo a los criterios de selección de AIC y BIC:
Como era de esperar, el Cuantil 0.95 tiene un coeficiente positivo en el modelo, ya que ante un aumento de la temperatura, aumenta la mortalidad y del mismo modo, la variable indicadora de covid tiene un coeficiente positivo. En la diagnosis del modelo, además de analizar la significación de los coeficientes, se ha comprobado que los residuos no están autocorrelados y que su distribución sigue una Normal.

Por lo tanto, se acepta el modelo tras haber superado satisfactoriamente todos los tests y para realizar el análisis del impacto que podría tener el cambio climático en la mortalidad solamente es necesario un último paso: calcular los posibles valores que la variable externa (el cuantil 0.95) puede tomar.
Para ello, se realiza un análisis de la serie temporal, solventando la no estacionariedad mediante una única diferenciación de la serie. Realizando un análisis similar al anterior, el modelo seleccionado es en este caso un arima(0,1,1). El cual obtiene los mejores resultados en AIC y BIC y supera todos los tests relacionados con la significación del coeficiente y los tests relacionados con los residuos a excepción de uno: el test de Anderson-Darling. Este test se emplea para probar que los residuos siguen una distribución Normal, al igual que los de Cramer von Mises y Jarque Bera, pero a diferencia de estos dos, presta especial atención a las colas de las distribuciones. Es decir, que, aunque los residuos sí siguiesen una distribución Normal de acuerdo con los tests de Cramer con mises y de Jarque Bera, en la cola de la distribución (la parte que más nos interesa en este caso) no sigue una distribución Normal.
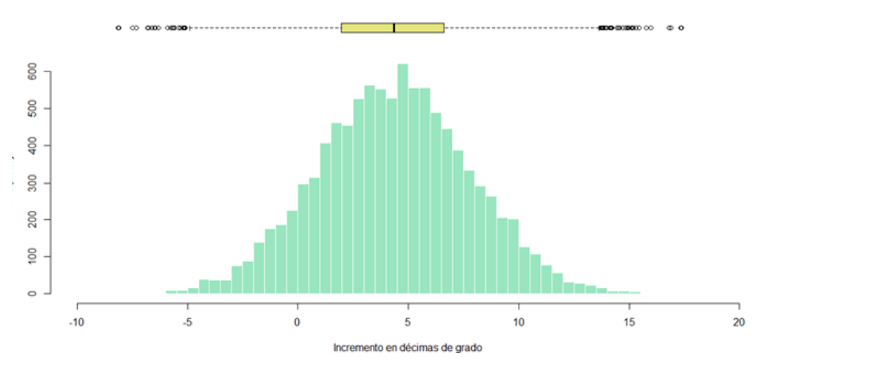
Esto último conlleva que, para la generación de escenarios de valores de la medida de temperatura, no se puede asumir normalidad, sino que será necesaria la generación de la distribución de probabilidad mediante bootstrapping. Tras realizar esta técnica, se obtienen 10,000 posibles escenarios entre los cuales se selecciona el Value at Risk al 99.5%:
Una vez obtenido el Value at Risk al 99.5%, es decir el peor escenario esperable de cada 200 escenarios, se puede emplear en el modelo anterior para obtener el índice de mortalidad y calcular la mortalidad.
El resultado de este incremento de 13.41 décimas de grado en el cuantil 0.95, conllevaría un incremento de la mortalidad de las personas más vulnerables (80 o más años) de un 3.20 % aproximadamente comparada con la mortalidad registrada en el año 2021 (año con gran incidencia de covid). Si comparamos las tasas resultantes con las del año 2019, en el cual los datos no se distorsionaron por el covid, estaríamos ante un incremento del 12.13 %.
Es importante destacar que cuando se habla del cambio climático se hace referencia a un riesgo comonótono, difícilmente diversificable. Empleando la visión holística del riesgo que plantea Solvencia II, se reflexiona que debería dársele una mayor importancia, cambiando su única presencia en el ORSA del Pilar II por su presencia en el Pilar I, para proteger los intereses de los asegurados, cumpliendo así la función social de los actuarios.
Finalmente, para poder cumplir esta función social asignada a los actuarios, se precisan de más investigaciones que, como esta, traten de mejorar las metodologías actuales para poder cuantificar el riesgo climático. En este trabajo, una nueva medida, el cuantil 0.95 es propuesta y se prueba cómo se relaciona más con la mortalidad que la empleada actualmente (media). Sin embargo, futuras líneas de investigación podrían tratar de relacionar esta medida con el factor de mejor de mortalidad de las tablas PASEM2020 además de seguir proporcionando estimaciones para concienciar a la población ante una de las principales amenazas de la humanidad.
Bibliography
Collier, S. J.-K. (2021). Climate change and insurance. Economy and Society, 50(2), 158-172. doi:https://www.tandfonline.com/doi/full/10.1080/03085147.2021.1903771
Huang, C. B. (2011). Projecting Future Heat-Related Mortality under Climate Change Scenarios: A Systematic Review. Environmental health perspectives(119), 1681-90. doi:https://ehp.niehs.nih.gov/doi/10.1289/ehp.1103456
Seklecka, M. P. (2017). Mortality effects of temperature changes in the United Kingdom. Journal of Forecasting(36(7)), 824-841. doi:https://onlinelibrary.wiley.com/doi/10.1002/for.2473



